Partition and Cover Field Tree

1. Home
2. Project: Partition and Cover Field Tree

---

Introduction

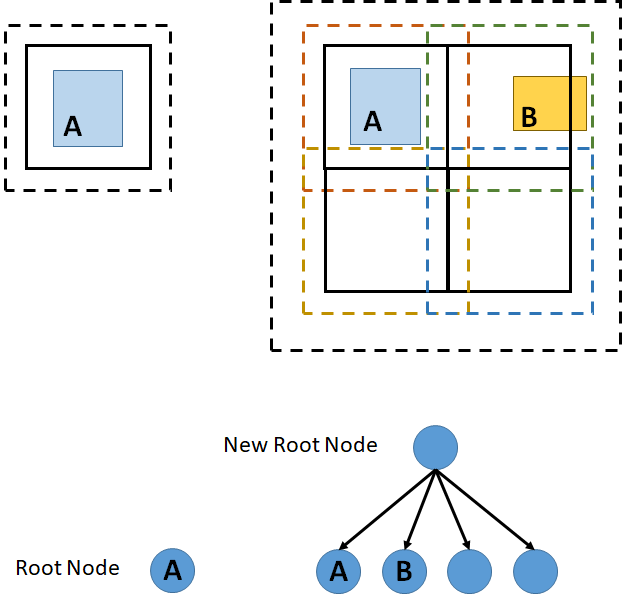
Various data structures exist for storing spatial objects. Quadtrees are the most popular structures for storing points and lines. Storing objects like rectangles becomes more challenging due to decisions regarding big objects. For this MX-CIF Quadtree can be very beneficial. In MX-CIF Quadtree, each object can be stored in a node that can completely encapsulate it. Therefore, an object cannot be stored in multiple nodes. This causes a space efficiency problem. To understand this better, let’s look at the following schematic in Fig. 1. When object A is added to the tree, it can be stored in the root, as the tree is empty. Adding object B, causes the root to overflow and requires partitioning. However, Both objects A and B intersect with multiple children, so neither can sink down to lower levels, hence storing becomes inefficient.

To Solve this problem and improve the efficiency for storing spatial objects, the following structures were designed:

• Cover (Loose) Field Tree

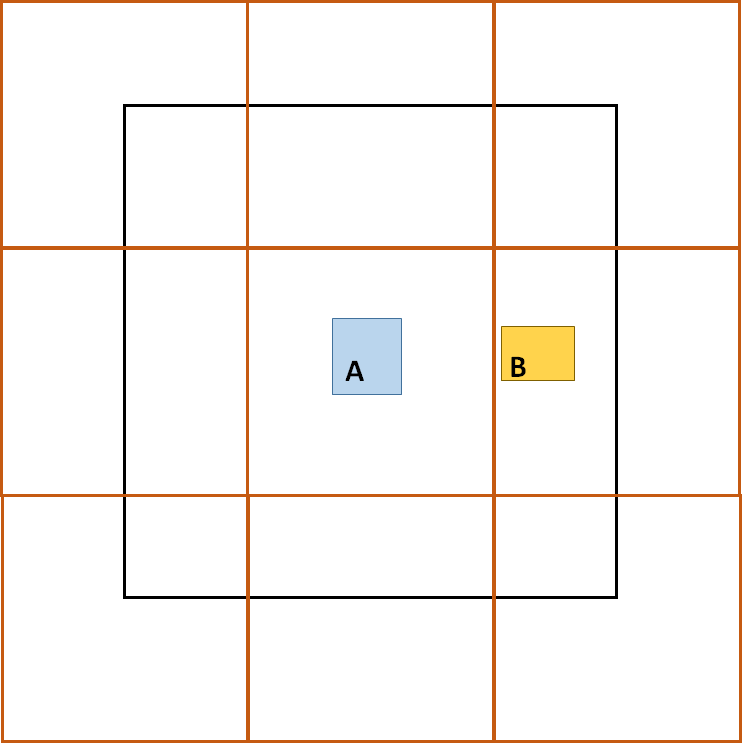
  In cover field tree, each node is expanded by (1 + p) where p is a value between 0 and 1. This expansion allows for objects (e.g. A and B) to sink further into the tree as shown in Fig. 2. As it can be seen now object A can sink into the expanded black quadrant, and object B has a choice of sinking in either blue or green quadrants. This choice brings the next problem, as the search for B requires to consider both quadrants. However, this tie can be broken by considering where the center of B lies. Using this convention, we can see the center of B is in original blue quadrant (not expanded quadrant), and hence by convention, we can choose quadrant blue as the storing node.

  

• Partition Field Tree

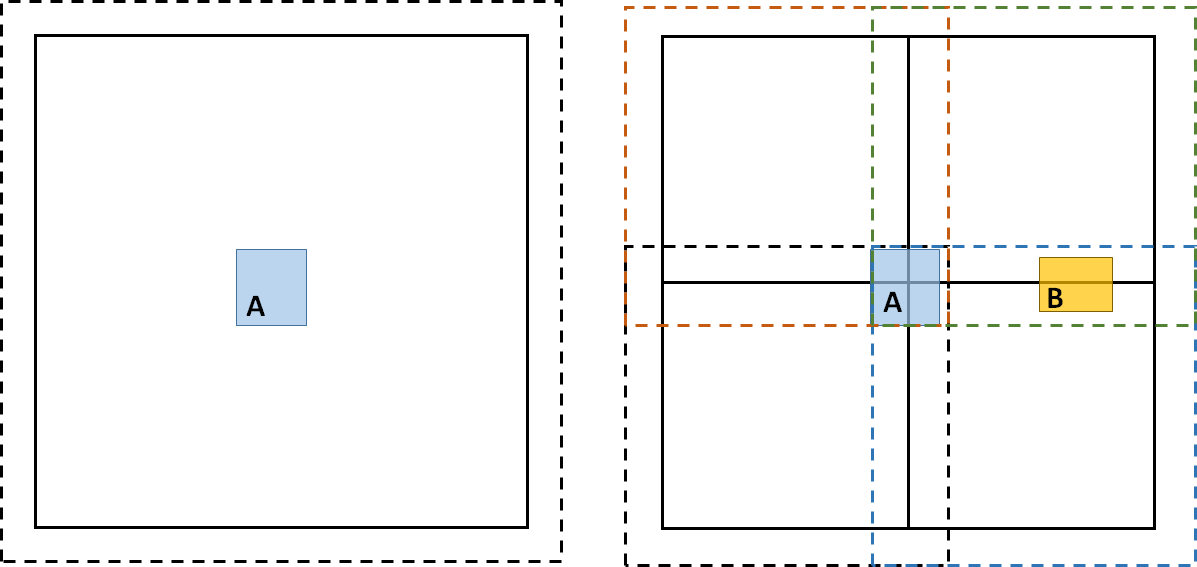
  As we observed in the cover field tree, the expanded nodes always overlap. To account for this partition field tree is designed based on nonoverlapping regions. In partition field tree, the children are still a quarter of the size of the parent, however, they are shifted by half their size in both x and y directions. This brings the complication in the data structure, as each node now has 9 children, while each child can have up to 4 parents (center child has 1 parent, edge children have 2 parents, and corner children have 4 parents each). This is shown in Fig 3.

  

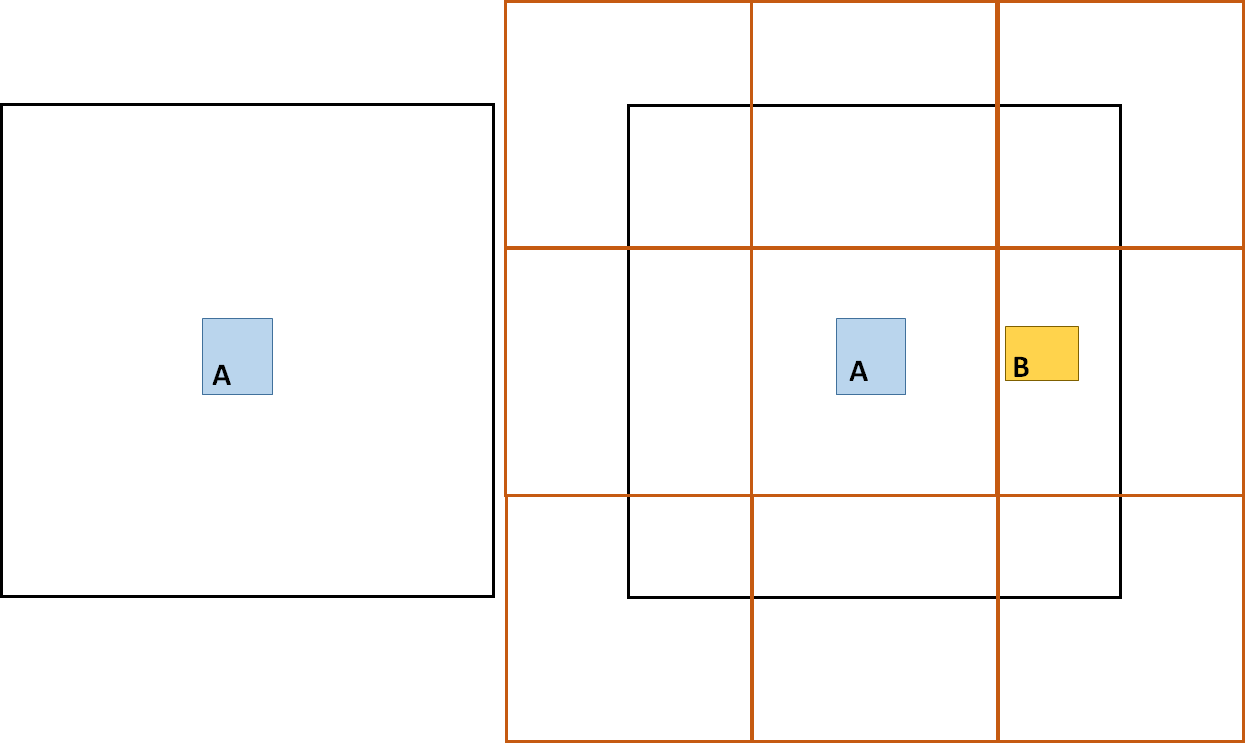
  As it can be seen now both objects A and B can sink to lower tree levels, and there will be no overlap between the nodes.

For implementation purposes, it must be noted that, since children share parents, some of the children may already exist if a neighboring parent has already partitioned. Therefore, it is necessary to search for existing children before creating all the children. A similar situation needs to be considered when deleting objects and merging nodes. Merging can cause children of neighboring parents to become incomplete, therefore a good convention can be merging children of a node if all siblings of the center node are either empty or non-existent.

Bottom-up trees

As is the problem with all quadtrees, the size of the space (width and height), needs to be known to create the root node. This brings a problem that such data structures are not suitable for applications with dynamic space size. Hence, the design of a bottom-up quadtree can be beneficial here. In this project, bottom-up cover field tree is discussed and implemented. In bottom-up cover field tree, the tree is initially empty and there is no root node. When adding object A, an encapsulating node with a size of power of 2 is being created as the root node. Upon adding object B, since B is not encapsulated by the root node, a new parent in the direction to encapsulate B is being created. The new root then creates the remaining children. This way, the structure has high space efficiency and can grow in both directions (smaller and bigger) to accommodate new objects. This is shown in Fig. 4.